Aasta 2007. Haridusministeeriumisse laekub lastevanemate avaldus põhikooli eksamitulemuste võltsimise kohta ühes Läänemaa gümnaasiumis. Direktor vabastatakse ametist, õpetaja saab trahvi. 

Talv 2025 – taas lahvatab skandaal. Anonüümseks jääda sooviv matemaatikaõpetaja teeb avalikuks tõsiasja, et juba aastaid on staažikas õpetaja ühes Tallinna gümnaasiumis „aidanud“ õpilasi eksami sooritamisel – et õpilane saaks mingilgi viisil nõutud punktid kätte ja lõpetaks kooli. Õpetaja ei eita süüd, ta vabastatakse töölt. Samal eksamil viibinud eksamikomisjoni esimees polevat aga mingeid rikkumisi märganud ja veidral kombel pole ka anonüümne matemaatikaõpetaja lasknud eksamiprotokolli kirjutada oma eriarvamust tööde ebaausa hindamise või eksamil aset leidnud õpetajapoolse etteütlemise kohta.  

Kaks täiesti erinevat, kuid sama mustriga juhtumit. Kas tegemist on avalikuks tulnud erandlike juhtumitega või on eksamitööde „loominguline“ parandamine laialt levinud ja vaikimisi heakskiidu leidnud? 

Aastal 2022, kui kooli lõpetamine ei sõltunud eksami tulemusest, mingeid anomaaliaid tulemuste jaotuses märgata pole. Seda ei saa aga öelda kahe viimase aasta tulemuste kohta, kus imeväel on olematuks muutunud 24 punkti saajate hulk ja väga taibukad põhikoolilõpetajad on suutnud töö kirjutada täpselt nii, et vajalik 25 punkti tuleks kokku ja 50% piir oleks ületatud. 

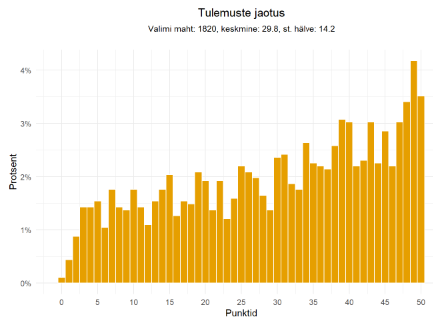
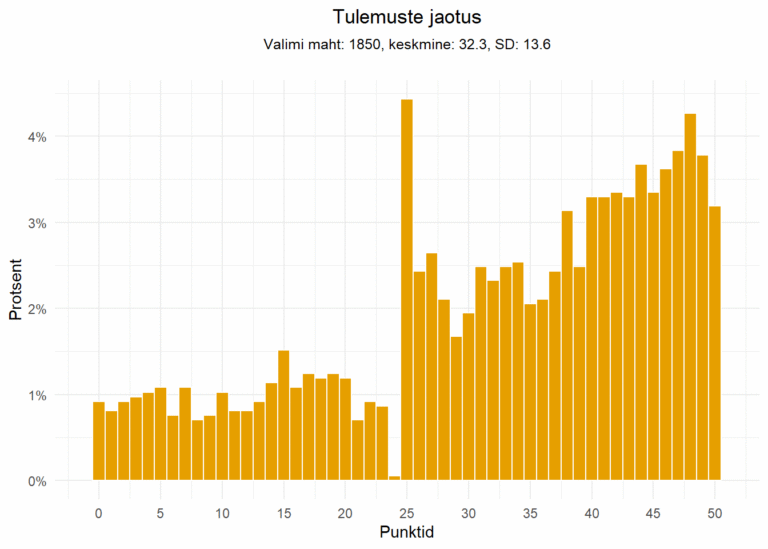
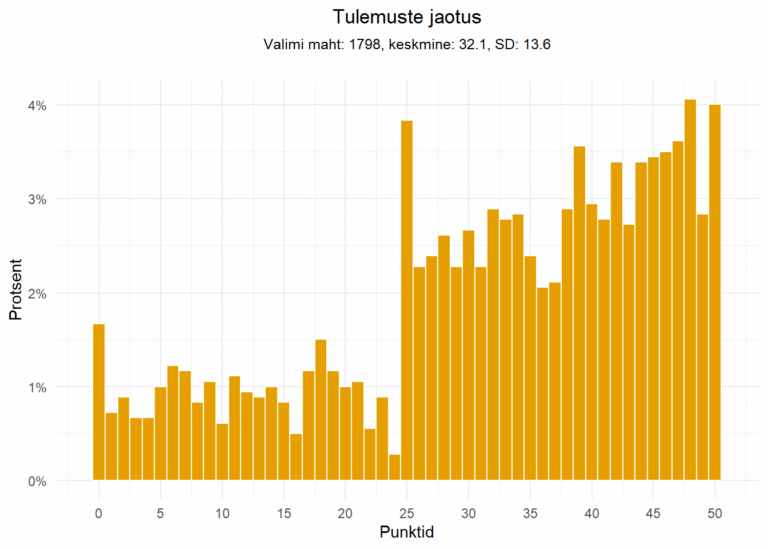
Harno matemaatika peaspetsialist Harlet Arismaa kirjutas selle kohta: „Käesoleva aasta tulemuste juures on jälle selgelt eristatav õpetajate hindamisefekt, kus tõenäoliselt otsitakse lävendi piiril oleva töö korral n-ö lisapunkti, mis väljendub tulemuste histogrammil iseloomuliku „korstnana“ lävendi (25 punkti) juures, seejuures 24 punktiga hinnatud töid on pea olematu arv.“ 

Siit küsimus: kas n-ö lisapunktide otsimine ja eksamitöö tulemuste kunstlik kergitamine ei vääri hukkamõistu? Ühe õpetaja naelutame häbiposti ja teistele vaatame läbi sõrmede. Kõik valimisse kuuluvad eksamitööd on Harnos olemas – missuguseid samme astuti ilmselgelt olematute punktide andmise tuvastamisel? Tõenäoliselt ei mingeid, fikseeriti olukord ja sellel kevadel kordub kõik taas. 

Tulemuste ilustamine (võltsimine) tööde parandajate poolt oli tuvastatav ka gümnaasiumi riigieksamite puhul. Seda senikaua, kuni lävendiks oli 20 punkti. Lävendi sisulise kaotamise järel (1% ei saa lugeda tõsiselt võetavaks või ületamatuks piiriks) kadus vajadus tulemustega manipuleerida. 

Aeg on muutusteks

Harno veebilehel olevad aruanded eksamite kohta on aastast aastasse nagu üksteise koopiad. Ikka on juttu sellest, et riik tahab teada, kuidas õppimine edeneb, missugune on kooli panus jne. Miskipärast pole poolt sõnagi õpilase panusest eksami edukal sooritamisel.

Aastaid tagasi olid eksami sooritamiseks erisused: üks osa õpilastest sooritas eksami 35% tulemuse korral. Mingil seletamatul põhjusel see erisus kaotati ja nüüd peab igal juhul 50% kätte saama. Kas või õpetaja abiga.

Head haridusametnikud, pekske õpetajat, sest ta ei ilmuta piisavalt professionaalsust ja õpilased kukuvad eksamil läbi. Ei saa pidada normaalseks, et veerand põhikoolilõpetajatest ei suuda matemaatikaeksamit õigel ajal sooritada. Pandeemia süüks nigelaid tulemusi panna ei saa, sest juba enne seda olid tulemused kehvad.

Harno matemaatika aruandes antakse soovitus: „Sõltuvalt õpilaste tasemest on soovitav lahendamiseks valida rohkem mittestandardseid ja rakendusliku sisuga ülesandeid, mis eeldavad teksti mõistmist ja loovalt lahendustee konstrueerimist, mitte väljakujunenud algoritmi rakendamist. Õpilaste funktsionaalse lugemisoskuse arendamiseks on soovitav lahendada ka pikema tekstiga ülesandeid.“

Pekske õpetajat, sest ta ei suuda seda teha. Kaasava hariduse tingimustes on ühes klassitoas need, kes valju häälega laulavad (neil on selline vajadus, ei tohi keelata), kes mängivad trummi (ka spetsiifiline vajadus), ja lõpuks ka need, kes soovivad tunnis midagigi kasulikku omandada. Andekatest lastest ma ei räägi, nendeni õpetaja koolitunni ajal ei jõuagi. Kui laps ei suuda lihtsatki teksti lugeda, siis missugusest ülesande lahenduse konstrueerimisest me räägime?

Õpetajana olen õnnelik, kui õpilane suudab kaks kahekohalist arvu kalkulaatori abil kokku liita ja pika pingutuse järel 5 cm pikkuse lõigu joonestada. Minu tähelepaneku põhjal on erivajadustega lapsed õnnetud, sest nad ei saa õpetaja jutust aru ega hakkagi aru saama. Sellest ka trots ja ebaadekvaatne käitumine. Väikeses rühmas õppides oleks nende tulemused oluliselt paremad.  

Muudame eksamite sisu ja vormi

On ilmselge, et vanaviisi edasi ei saa. Ma ei ole seda meelt, et jätame eksamid ära ja siis on kõik hästi. Ometigi, Soome õpilased ei tee põhikooli lõpus eksameid, kuid seal saavad komplekteeritud nii gümnaasiumid kui ka ametikoolid. Kas mitte sealt eeskuju võtta? 

Mõned sammud saab paari aastaga siiski ära teha (sealjuures unustagem igasugused e-eksamid, sest matemaatikas ei ole need lähitulevikus mõistlikul viisil realiseeritavad). Teen ettepaneku koostada eksam kahes osas: esimeses osas oleksid lühikesed ja lihtsa tekstiga ülesanded põhioskuste kohta ja teises ülesanded, mis nõuavad teksti sisulist mõistmist, lahendusplaani koostamist jne. Eksami sooritamiseks on vaja eksami esimene osa teha vähemalt rahuldavalt. 

Õpilased, kes mingil põhjusel ei saa õigel ajal eksamit sooritada (haige, võistlustel vms), teevad eksami hiljem ja ka nende puhul kasutatakse Harno koostatud ülesandeid – igasugune koolipoolne isetegevus järeleksamite (libaeksamite) näol tuleb ära lõpetada. Õige (põhieksamil saadud) tulemus tuleb kirjutada lõputunnistusele. Ükski eksam, test või mis tahes muu sooritus ei tohi tekitada olukorda, kus õpetaja peab õpilase tulevikku silmas pidades tulemusi moonutama, et laps saaks kooli lõpetatud. Eksami tulemus ja kooli lõpetamine ei peaks olema 9. klassis omavahel seotud. 

Kellele on eespool välja toodud seisukohad vastukarva ja kes tahab jätkata vanaviisi, see lasku käia. Pekske õpetajaid, kuni veel on, keda peksta! 

Artikli autor esitas oma isiklikke seisukohti, mis ei pruugi kokku langeda tööandja tõekspidamisega.